
An important property of any gas is its pressure. We have some experience with air pressure that we don't have with properties like viscosity and compressibility. We've heard meteorologists give the daily value of the barometric pressure of the atmosphere (29.8 inches of mercury, for example). And most of us have blown up a balloon or used a pump to inflate a bicycle tire or a basketball.
Because understanding what pressure is and how it works is so fundamental to the understanding of aerodynamics, we are including several slides on air pressure in the Beginner's Guide. An interactive simulator allows you to study how the atmospheric pressure changes with altitude.
Definition of Pressure
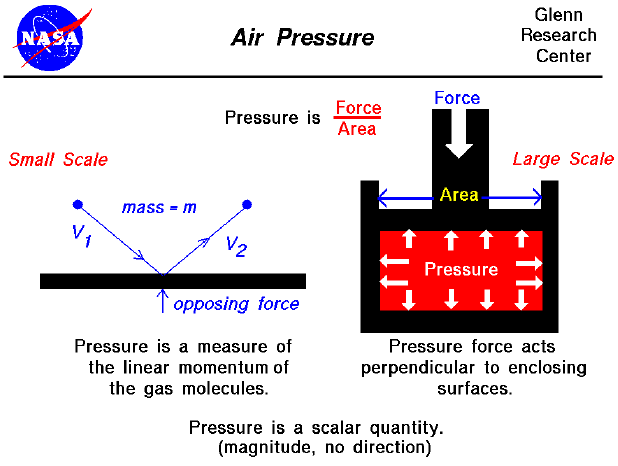
There are two ways to look at pressure: (1) the small scale action of individual air molecules or (2) the large scale action of a large number of molecules. Starting with the small scale action, from the kinetic theory of gases, a gas is composed of a large number of molecules that are very small relative to the distance between molecules. The molecules are in constant, random motion and frequently collide with each other and with the walls of any container. The molecules possess the physical properties of mass, momentum, and energy. As the gas molecules collide with the walls of a container, as shown on the left of the figure, the molecules impart momentum to the walls, producing a force perpendicular to the wall. The sum of the forces of all the molecules striking the wall divided by the area of the wall is defined to be the pressure. The pressure of a gas is then a measure of the linear momentum of the molecules of a gas. The pressure acts perpendicular (normal) to the wall; the tangential (shear) component of the force is related to the viscosity of the gas.
Scalar Quantity
Let us look at a gas that does not appear to move or flow. Actually, while the gas does not appear to move, the individual molecules of the gas (which we cannot see) are in constant random motion. Because we are dealing with a large number of molecules (nearly infinite) and because the motion of the individual molecules is random in every direction, we do not detect any motion. If we enclose the gas within a container, we will detect a pressure in the gas from the molecules colliding with the walls of our container. We can put the walls of our container anywhere inside the gas, and the force per area (the pressure) will be the same. (If the gas as a whole were moving, the measured pressure would be different in the direction of the motion, as described by Bernoulli's equation.) We could shrink the size of our "container" down to an infinitely small point, and the pressure would have a single value at that point. Therefore, pressure is a scalar quantity, not a vector quantity. It has a magnitude but no direction associated with it. Pressure acts in all directions at a point inside a gas. At the surface of a gas, the pressure force acts perpendicular to the surface.
Magnitude of Pressure Force
Turning to the larger scale, the magnitude of the pressure force is equal to the pressure (force/area) times the surface area, and the direction is perpendicular to the surface. (You can explore the effects of pressure on other gas variables at the animated gas lab). In the figure shown above on the right, we have a gas (in red) that is confined in a box. A force is applied to the top of the box. The pressure force within the box opposes the applied force. And the pressure equals the external force divided by the area of the top of the box. Inside the gas, the pressure acts in all directions. So the pressure would also push on the bottom of the box and on the sides. This is different from simple solid mechanics. If the red gas were a solid, there would be no forces applied to the sides of the box; the applied force would be simply transmitted to the bottom. But in a gas, because the molecules are free to move about and collide with one another, a force applied in the vertical direction causes forces in the horizontal direction.